Not All Independent Variables Can Be Retained in Binary Logits Brant Test Cannot Be Computed
Version info: Lawmaking for this page was tested in Stata 12.
Introduction
This page shows how to perform a number of statistical tests using Stata. Each department gives a cursory description of the aim of the statistical test, when it is used, an example showing the Stata commands and Stata output with a brief estimation of the output. You can see the page Choosing the Right Statistical Examination for a table that shows an overview of when each test is advisable to employ. In deciding which test is appropriate to employ, it is important to consider the type of variables that you lot accept (i.due east., whether your variables are categorical, ordinal or interval and whether they are normally distributed), see What is the divergence between categorical, ordinal and interval variables? for more than information on this.
Near the hsb information file
Most of the examples in this page volition employ a data file called hsb2, high schoolhouse and beyond. This data file contains 200 observations from a sample of high school students with demographic information about the students, such as their gender (female), socio-economic status (ses) and ethnic groundwork (race). It also contains a number of scores on standardized tests, including tests of reading (read), writing (write), mathematics (math) and social studies (socst). You lot tin can become the hsb2 information file from inside Stata past typing:
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2
1 sample t-exam
A one sample t-test allows u.s. to test whether a sample hateful (of a ordinarily distributed interval variable) significantly differs from a hypothesized value. For example, using the hsb2 data file, say we wish to examination whether the average writing score (write) differs significantly from 50. We tin do this as shown beneath.
ttest write=50
One-sample t test ------------------------------------------------------------------------------ Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval] ---------+-------------------------------------------------------------------- write | 200 52.775 .6702372 9.478586 51.45332 54.09668 ------------------------------------------------------------------------------ Degrees of freedom: 199 Ho: mean(write) = 50 Ha: mean < 50 Ha: mean ~= 50 Ha: mean > 50 t = iv.1403 t = four.1403 t = iv.1403 P < t = 1.0000 P > |t| = 0.0001 P > t = 0.0000
The mean of the variable write for this particular sample of students is 52.775, which is statistically significantly different from the exam value of 50. We would conclude that this group of students has a significantly college hateful on the writing test than 50.
See likewise
- Stata Code Fragment: Descriptives, ttests, Anova and Regression
- Stata Class Notes: Analyzing Data
One sample median test
A 1 sample median exam allows u.s.a. to test whether a sample median differs significantly from a hypothesized value. We volition apply the aforementioned variable, write, equally we did in the one sample t-test example in a higher place, simply we do not need to assume that it is interval and ordinarily distributed (nosotros only demand to assume that write is an ordinal variable and that its distribution is symmetric). We will test whether the median writing score (write) differs significantly from 50.
signrank write=fifty
Wilcoxon signed-rank examination sign | obs sum ranks expected -------------+--------------------------------- positive | 126 13429 10048.5 negative | 72 6668 10048.5 goose egg | ii 3 3 -------------+--------------------------------- all | 200 20100 20100 unadjusted variance 671675.00 adjustment for ties -1760.25 adjustment for zeros -i.25 --------- adjusted variance 669913.50 Ho: write = 50 z = 4.130 Prob > |z| = 0.0000
The results point that the median of the variable write for this group is statistically significantly different from 50.
Meet likewise
- Stata Code Fragment: Descriptives, ttests, Anova and Regression
Binomial exam
A i sample binomial test allows united states of america to test whether the proportion of successes on a 2-level categorical dependent variable significantly differs from a hypothesized value. For case, using the hsb2 data file, say we wish to exam whether the proportion of females (female) differs significantly from 50%, i.due east., from .5. We can practise this every bit shown beneath.
bitest female person=.5
Variable | Northward Observed k Expected k Assumed p Observed p -------------+------------------------------------------------------------ female | 200 109 100 0.50000 0.54500 Pr(k >= 109) = 0.114623 (one-sided test) Pr(thou <= 109) = 0.910518 (1-sided test) Pr(thousand <= 91 or k >= 109) = 0.229247 (two-sided exam)
The results indicate that there is no statistically significant difference (p = .2292). In other words, the proportion of females does not significantly differ from the hypothesized value of 50%.
Run into besides
Chi-square goodness of fit
A chi-foursquare goodness of fit test allows u.s.a. to test whether the observed proportions for a categorical variable differ from hypothesized proportions. For example, permit'southward suppose that we believe that the general population consists of 10% Hispanic, 10% Asian, 10% African American and 70% White folks. Nosotros want to examination whether the observed proportions from our sample differ significantly from these hypothesized proportions. To conduct the chi-square goodness of fit test, y'all need to first download the csgof plan that performs this test. You lot can download csgof from within Stata past typing search csgof (see How can I used the search control to search for programs and get boosted help? for more information about using search).
Now that the csgof program is installed, we can utilize it by typing:
csgof race, expperc(ten 10 10 70) race expperc expfreq obsfreq hispanic ten twenty 24 asian 10 twenty 11 african-amer ten 20 20 white lxx 140 145 chisq(iii) is v.03, p = .1697
These results prove that racial limerick in our sample does not differ significantly from the hypothesized values that we supplied (chi-square with three degrees of freedom = 5.03, p = .1697).
Run across besides
- Useful Stata Programs
Two independent samples t-test
An independent samples t-exam is used when you desire to compare the means of a normally distributed interval dependent variable for two contained groups. For example, using the hsb2 data file, say we wish to test whether the mean for write is the same for males and females.
ttest write, past(female) Two-sample t test with equal variances ------------------------------------------------------------------------------ Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval] ---------+-------------------------------------------------------------------- male | 91 50.12088 ane.080274 ten.30516 47.97473 52.26703 female person | 109 54.99083 .7790686 viii.133715 53.44658 56.53507 ---------+-------------------------------------------------------------------- combined | 200 52.775 .6702372 ix.478586 51.45332 54.09668 ---------+-------------------------------------------------------------------- unequal | -4.869947 1.304191 -7.441835 -2.298059 ------------------------------------------------------------------------------ Degrees of liberty: 198 Ho: mean(male) - mean(female) = diff = 0 Ha: unequal < 0 Ha: diff ~= 0 Ha: unequal > 0 t = -3.7341 t = -3.7341 t = -3.7341 P < t = 0.0001 P > |t| = 0.0002 P > t = 0.9999
The results bespeak that at that place is a statistically significant difference between the hateful writing score for males and females (t = -three.7341, p = .0002). In other words, females have a statistically significantly higher hateful score on writing (54.99) than males (50.12).
Run across also
- Stata Learning Module: A Statistical Sampler in Stata
- Stata Form Notes: Analyzing Data
Wilcoxon-Mann-Whitney examination
The Wilcoxon-Mann-Whitney test is a non-parametric analog to the independent samples t-test and can be used when you do not presume that the dependent variable is a normally distributed interval variable (you simply assume that the variable is at least ordinal). You will notice that the Stata syntax for the Wilcoxon-Mann-Whitney exam is almost identical to that of the contained samples t-examination. We will use the aforementioned information file (the hsb2 information file) and the same variables in this example as nosotros did in the independent t-test example in a higher place and volition non presume that write, our dependent variable, is normally distributed.
ranksum write, by(female)
Two-sample Wilcoxon rank-sum (Isle of mann-Whitney) test female | obs rank sum expected -------------+--------------------------------- male | 91 7792 9145.five female | 109 12308 10954.v -------------+--------------------------------- combined | 200 20100 20100 unadjusted variance 166143.25 adjustment for ties -852.96 ---------- adjusted variance 165290.29 Ho: write(female==male) = write(female==female) z = -three.329 Prob > |z| = 0.0009
The results suggest that there is a statistically meaning divergence between the underlying distributions of the write scores of males and the write scores of females (z = -3.329, p = 0.0009). You can determine which grouping has the higher rank by looking at the how the bodily rank sums compare to the expected rank sums nether the null hypothesis. The sum of the female ranks was higher while the sum of the male ranks was lower. Thus the female grouping had higher rank.
See also
- FAQ: Why is the Mann-Whitney significant when the medians are equal?
- Stata Grade Notes: Analyzing Information
Chi-square exam
A chi-foursquare test is used when y'all want to see if at that place is a relationship between ii categorical variables. In Stata, the chi2 option is used with the tabulate command to obtain the exam statistic and its associated p-value. Using the hsb2 data file, let's see if in that location is a relationship betwixt the type of school attended (schtyp) and students' gender (female). Remember that the chi-foursquare test assumes the expected value of each cell is five or higher. This supposition is easily met in the examples below. Still, if this assumption is non met in your data, please encounter the section on Fisher's exact test beneath.
tabulate schtyp female person, chi2 blazon of | female person school | male person female | Total -----------+----------------------+---------- public | 77 91 | 168 private | 14 18 | 32 -----------+----------------------+---------- Total | 91 109 | 200 Pearson chi2(ane) = 0.0470 Pr = 0.828
These results indicate that there is no statistically significant relationship between the type of school attended and gender (chi-square with one caste of freedom = 0.0470, p = 0.828).
Let'due south look at another example, this time looking at the relationship between gender (female person) and socio-economic condition (ses). The point of this example is that 1 (or both) variables may have more than two levels, and that the variables do non have to accept the same number of levels. In this instance, female has two levels (male and female) and ses has 3 levels (depression, medium and high).
tabulate female ses, chi2 | ses female person | depression middle high | Total -----------+---------------------------------+---------- male | 15 47 29 | 91 female | 32 48 29 | 109 -----------+---------------------------------+---------- Total | 47 95 58 | 200 Pearson chi2(two) = 4.5765 Pr = 0.101
Over again nosotros find that in that location is no statistically significant relationship between the variables (chi-square with 2 degrees of liberty = 4.5765, p = 0.101).
See also
- Stata Learning Module: A Statistical Sampler in Stata
- Stata Teaching Tools: Probability Tables
- Stata Educational activity Tools: Chi-squared distribution
- Stata Textbook Examples: An Introduction to Chiselled Analysis, Chapter 2
Fisher'due south exact examination
The Fisher'southward exact exam is used when you want to carry a chi-square test, simply one or more of your cells has an expected frequency of five or less. Remember that the chi-square test assumes that each cell has an expected frequency of five or more, merely the Fisher'southward verbal test has no such assumption and can exist used regardless of how small the expected frequency is. In the instance below, we have cells with observed frequencies of two and 1, which may point expected frequencies that could be beneath five, and so we will use Fisher's exact test with the exact selection on the tabulate command.
tabulate schtyp race, exact type of | race school | hispanic asian african-a white | Total -----------+--------------------------------------------+---------- public | 22 10 18 118 | 168 private | 2 1 2 27 | 32 -----------+--------------------------------------------+---------- Full | 24 eleven 20 145 | 200 Fisher'southward verbal = 0.597
These results advise that there is not a statistically meaning human relationship between race and type of school (p = 0.597). Note that the Fisher'due south exact exam does not have a "test statistic", but computes the p-value directly.
Come across likewise
- Stata Learning Module: A Statistical Sampler in Stata
- Stata Textbook Examples: Statistical Methods for the Social Sciences, Chapter 7
One-way ANOVA
A 1-mode analysis of variance (ANOVA) is used when you lot have a categorical independent variable (with 2 or more categories) and a normally distributed interval dependent variable and you wish to test for differences in the ways of the dependent variable broken downwards past the levels of the contained variable. For example, using the hsb2 data file, say we wish to exam whether the hateful of write differs between the 3 program types (prog). The command for this examination would be:
anova write prog Number of obs = 200 R-squared = 0.1776 Root MSE = 8.63918 Adj R-squared = 0.1693 Source | Fractional SS df MS F Prob > F -----------+---------------------------------------------------- Model | 3175.69786 2 1587.84893 21.27 0.0000 | prog | 3175.69786 two 1587.84893 21.27 0.0000 | Residual | 14703.1771 197 74.635417 -----------+---------------------------------------------------- Total | 17878.875 199 89.843593
The mean of the dependent variable differs significantly among the levels of programme type. Nevertheless, we do non know if the deviation is between only ii of the levels or all 3 of the levels. (The F test for the Model is the same as the F exam for prog because prog was the just variable entered into the model. If other variables had also been entered, the F exam for the Model would have been different from prog.) To run across the mean of write for each level of program blazon, you can apply the tabulate control with the summarize option, as illustrated below.
tabulate prog, summarize(write) type of | Summary of writing score program | Mean Std. Dev. Freq. ------------+------------------------------------ full general | 51.333333 ix.3977754 45 academic | 56.257143 7.9433433 105 vocation | 46.76 9.3187544 50 ------------+------------------------------------ Full | 52.775 9.478586 200
From this we can run across that the students in the academic programme take the highest mean writing score, while students in the vocational plan take the lowest.
Come across also
- Design and Assay: A Researchers Handbook Third Edition by Geoffrey Keppel
- Stata Frequently Asked Questions
- Stata Programs for Data Assay
Kruskal Wallis test
The Kruskal Wallis exam is used when you have i independent variable with two or more than levels and an ordinal dependent variable. In other words, it is the not-parametric version of ANOVA and a generalized form of the Isle of man-Whitney test method since it permits 2 or more than groups. We will use the aforementioned data file every bit the 1 way ANOVA example above (the hsb2 data file) and the aforementioned variables equally in the example in a higher place, but we volition not assume that write is a normally distributed interval variable.
kwallis write, by(prog)
Test: Equality of populations (Kruskal-Wallis exam) prog _Obs _RankSum full general < 45 4079.00 academic 105 12764.00 vocation 50 3257.00 chi-squared = 33.870 with 2 d.f. probability = 0.0001 chi-squared with ties = 34.045 with 2 d.f. probability = 0.0001
If some of the scores receive tied ranks, then a correction gene is used, yielding a slightly different value of chi-squared. With or without ties, the results bespeak that there is a statistically pregnant difference amid the three blazon of programs.
Paired t-test
A paired (samples) t-exam is used when you have two related observations (i.e. two observations per subject) and you lot want to come across if the ways on these 2 normally distributed interval variables differ from ane another. For case, using the hsb2 data file we will test whether the hateful of read is equal to the hateful of write.
ttest read = write
Paired t test ------------------------------------------------------------------------------ Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval] ---------+-------------------------------------------------------------------- read | 200 52.23 .7249921 ten.25294 50.80035 53.65965 write | 200 52.775 .6702372 9.478586 51.45332 54.09668 ---------+-------------------------------------------------------------------- diff | 200 -.545 .6283822 eight.886666 -i.784142 .6941424 ------------------------------------------------------------------------------ Ho: mean(read - write) = hateful(diff) = 0 Ha: mean(diff) < 0 Ha: mean(diff) ~= 0 Ha: mean(diff) > 0 t = -0.8673 t = -0.8673 t = -0.8673 P < t = 0.1934 P > |t| = 0.3868 P > t = 0.8066
These results point that the mean of read is not statistically significantly different from the mean of write (t = -0.8673, p = 0.3868).
See also
- Stata Learning Module: Comparing Stata and SAS Side by Side
Wilcoxon signed rank sum test
The Wilcoxon signed rank sum test is the non-parametric version of a paired samples t-examination. Yous employ the Wilcoxon signed rank sum test when y'all do not wish to assume that the difference betwixt the two variables is interval and normally distributed (but you do assume the difference is ordinal). We volition use the same example equally higher up, just we volition not assume that the difference between read and write is interval and normally distributed.
signrank read = write
Wilcoxon signed-rank test sign | obs sum ranks expected -------------+--------------------------------- positive | 88 9264 9990 negative | 97 10716 9990 zero | 15 120 120 -------------+--------------------------------- all | 200 20100 20100 unadjusted variance 671675.00 adjustment for ties -715.25 adjustment for zeros -310.00 ---------- adjusted variance 670649.75 Ho: read = write z = -0.887 Prob > |z| = 0.3753
The results suggest that there is not a statistically meaning difference betwixt read and write.
If you believe the differences between read and write were not ordinal but could merely be classified every bit positive and negative, then yous may want to consider a sign exam in lieu of sign rank test. Once again, we will utilise the same variables in this example and presume that this difference is not ordinal.
signtest read = write
Sign exam sign | observed expected -------------+------------------------ positive | 88 92.5 negative | 97 92.five nix | 15 15 -------------+------------------------ all | 200 200 I-sided tests: Ho: median of read - write = 0 vs. Ha: median of read - write > 0 Pr(#positive >= 88) = Binomial(n = 185, x >= 88, p = 0.5) = 0.7688 Ho: median of read - write = 0 vs. Ha: median of read - write < 0 Pr(#negative >= 97) = Binomial(n = 185, x >= 97, p = 0.five) = 0.2783 Two-sided examination: Ho: median of read - write = 0 vs. Ha: median of read - write ~= 0 Pr(#positive >= 97 or #negative >= 97) = min(one, 2*Binomial(due north = 185, 10 >= 97, p = 0.5)) = 0.5565
This output gives both of the one-sided tests equally well equally the two-sided test. Assuming that we were looking for any difference, we would apply the two-sided test and conclude that no statistically significant difference was found (p=.5565).
See also
- Stata Code Fragment: Descriptives, ttests, Anova and Regression
- Stata Form Notes: Analyzing Data
McNemar exam
You would perform McNemar's test if you were interested in the marginal frequencies of two binary outcomes. These binary outcomes may be the aforementioned outcome variable on matched pairs (like a case-control report) or two outcome variables from a unmarried group. For case, allow usa consider ii questions, Q1 and Q2, from a examination taken by 200 students. Suppose 172 students answered both questions correctly, fifteen students answered both questions incorrectly, vii answered Q1 correctly and Q2 incorrectly, and 6 answered Q2 correctly and Q1 incorrectly. These counts can be considered in a two-way contingency table. The nothing hypothesis is that the two questions are answered correctly or incorrectly at the same rate (or that the contingency tabular array is symmetric). We can enter these counts into Stata using mcci, a command from Stata'due south epidemiology tables. The result is labeled according to case-control study conventions.
mcci 172 6 7 15
| Controls | Cases | Exposed Unexposed | Total -----------------+------------------------+------------ Exposed | 172 6 | 178 Unexposed | 7 15 | 22 -----------------+------------------------+------------ Total | 179 21 | 200 McNemar'south chi2(1) = 0.08 Prob > chi2 = 0.7815 Verbal McNemar significance probability = 1.0000 Proportion with cistron Cases .89 Controls .895 [95% Conf. Interval] --------- -------------------- divergence -.005 -.045327 .035327 ratio .9944134 .9558139 i.034572 rel. diff. -.047619 -.39205 .2968119 odds ratio .8571429 .2379799 two.978588 (exact)
McNemar's chi-square statistic suggests that in that location is not a statistically significant difference in the proportions of correct/incorrect answers to these 2 questions.
One-way repeated measures ANOVA
You would perform a one-fashion repeated measures analysis of variance if yous had one categorical independent variable and a unremarkably distributed interval dependent variable that was repeated at least twice for each subject field. This is the equivalent of the paired samples t-examination, but allows for two or more levels of the categorical variable. This tests whether the mean of the dependent variable differs past the categorical variable. We accept an instance data set called rb4, which is used in Kirk'southward book Experimental Blueprint. In this data set, y is the dependent variable, a is the repeated measure and south is the variable that indicates the subject area number.
use https://stats.idre.ucla.edu/stat/stata/examples/kirk/rb4 anova y a southward, repeated(a)
Number of obs = 32 R-squared = 0.7318 Root MSE = ane.18523 Adj R-squared = 0.6041 Source | Fractional SS df MS F Prob > F -----------+---------------------------------------------------- Model | eighty.50 ten viii.05 v.73 0.0004 | a | 49.00 iii sixteen.3333333 11.63 0.0001 due south | 31.50 seven 4.50 3.20 0.0180 | Rest | 29.l 21 one.4047619 -----------+---------------------------------------------------- Total | 110.00 31 3.5483871 Between-subjects error term: s Levels: viii (7 df) Lowest b.s.eastward. variable: s Repeated variable: a Huynh-Feldt epsilon = 0.8343 Greenhouse-Geisser epsilon = 0.6195 Box's conservative epsilon = 0.3333 ------------ Prob > F ------------ Source | df F Regular H-F K-K Box -----------+---------------------------------------------------- a | three 11.63 0.0001 0.0003 0.0015 0.0113 Rest | 21 -----------+----------------------------------------------------
You volition notice that this output gives four different p-values. The "regular" (0.0001) is the p-value that you would get if you assumed chemical compound symmetry in the variance-covariance matrix. Because that supposition is often not valid, the 3 other p-values offer various corrections (the Huynh-Feldt, H-F, Greenhouse-Geisser, G-G and Box'due south conservative, Box). No thing which p-value y'all use, our results indicate that we accept a statistically pregnant effect of a at the .05 level.
Run across also
- Stata FAQ: How can I test for nonadditivity in a randomized block ANOVA in Stata?
- Stata Textbook Examples, Experimental Pattern, Affiliate 7
- Stata Code Fragment: ANOVA
Repeated measures logistic regression
If you have a binary outcome measured repeatedly for each subject and you wish to run a logistic regression that accounts for the effect of these multiple measures from each subjects, you can perform a repeated measures logistic regression. In Stata, this can be done using the xtgee command and indicating binomial as the probability distribution and logit as the link role to be used in the model. The exercise information file contains 3 pulse measurements of xxx people assigned to 2 dissimilar diet regiments and 3 different exercise regiments. If we define a "loftier" pulse as being over 100, nosotros can then predict the probability of a loftier pulse using nutrition regiment.
Showtime, nosotros use xtset to define which variable defines the repetitions. In this dataset, there are 3 measurements taken for each id, then we will utilise id as our panel variable. And so we tin can use i: before diet so that nosotros can create indicator variables every bit needed.
use https://stats.idre.ucla.edu/stat/stata/whatstat/practice, articulate xtset id xtgee highpulse i.diet, family(binomial) link(logit)
Iteration 1: tolerance = 1.753e-08 GEE population-averaged model Number of obs = 90 Group variable: id Number of groups = 30 Link: logit Obs per group: min = 3 Family: binomial avg = iii.0 Correlation: exchangeable max = 3 Wald chi2(1) = 1.53 Calibration parameter: one Prob > chi2 = 0.2157 ------------------------------------------------------------------------------ highpulse | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- 2.nutrition | .7537718 .6088196 one.24 0.216 -.4394927 1.947036 _cons | -one.252763 .4621704 -2.71 0.007 -2.1586 -.3469257 ------------------------------------------------------------------------------
These results point that diet is non statistically significant (Z = 1.24, p = 0.216).
Factorial ANOVA
A factorial ANOVA has ii or more than categorical contained variables (either with or without the interactions) and a single ordinarily distributed interval dependent variable. For example, using the hsb2 data file we will expect at writing scores (write) every bit the dependent variable and gender (female) and socio-economic status (ses) as independent variables, and nosotros will include an interaction of female past ses. Notation that in Stata, you practise non need to take the interaction term(s) in your data set. Rather, you tin accept Stata create information technology/them temporarily by placing an asterisk betwixt the variables that will make up the interaction term(southward).
anova write female ses female##ses Number of obs = 200 R-squared = 0.1274 Root MSE = eight.96748 Adj R-squared = 0.1049 Source | Fractional SS df MS F Prob > F -----------+---------------------------------------------------- Model | 2278.24419 5 455.648837 5.67 0.0001 | female | 1334.49331 i 1334.49331 16.59 0.0001 ses | 1063.2527 2 531.626349 half-dozen.61 0.0017 female#ses | 21.4309044 two 10.7154522 0.13 0.8753 | Residual | 15600.6308 194 80.4156228 -----------+---------------------------------------------------- Full | 17878.875 199 89.843593
These results indicate that the overall model is statistically significant (F = 5.67, p = 0.001). The variables female person and ses are also statistically significant (F = 16.59, p = 0.0001 and F = 6.61, p = 0.0017, respectively). However, that interaction between female and ses is not statistically significant (F = 0.13, p = 0.8753).
Encounter also
- Stata Ofttimes Asked Questions
- Stata Textbook Examples, Experimental Design, Chapter 9
- Stata Lawmaking Fragment: ANOVA
Friedman exam
You perform a Friedman test when you have one within-subjects independent variable with two or more levels and a dependent variable that is non interval and unremarkably distributed (but at least ordinal). We will use this test to determine if at that place is a difference in the reading, writing and math scores. The null hypothesis in this test is that the distribution of the ranks of each blazon of score (i.e., reading, writing and math) are the same. To conduct the Friedman test in Stata, yous demand to first download the friedman program that performs this examination. Yous can download friedman from within Stata by typing search friedman (see How can I used the search command to search for programs and become additional help? for more information most using search). Also, your data will need to exist transposed such that subjects are the columns and the variables are the rows. We will use the xpose command to adjust our data this mode.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2 proceed read write math xpose, clear friedman v1-v200
Friedman = 0.6175 Kendall = 0.0015 P-value = 0.7344
Friedman's chi-square has a value of 0.6175 and a p-value of 0.7344 and is not statistically significant. Hence, there is no evidence that the distributions of the 3 types of scores are different.
Ordered logistic regression
Ordered logistic regression is used when the dependent variable is ordered, merely non continuous. For instance, using the hsb2 information file nosotros will create an ordered variable called write3. This variable will have the values 1, ii and three, indicating a depression, medium or high writing score. We do not generally recommend categorizing a continuous variable in this way; we are simply creating a variable to use for this case. We volition use gender (female), reading score (read) and social studies score (socst) as predictor variables in this model.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2 generate write3 = 1 replace write3 = ii if write >= 49 & write <= 57 supersede write3 = 3 if write >= 58 & write <= seventy
ologit write3 female read socst Iteration 0: log likelihood = -218.31357 Iteration ane: log likelihood = -157.692 Iteration 2: log likelihood = -156.28133 Iteration 3: log likelihood = -156.27632 Iteration 4: log likelihood = -156.27632 Ordered logistic regression Number of obs = 200 LR chi2(3) = 124.07 Prob > chi2 = 0.0000 Log likelihood = -156.27632 Pseudo R2 = 0.2842 ------------------------------------------------------------------------------ write3 | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- female | ane.285435 .3244567 3.96 0.000 .6495115 1.921359 read | .1177202 .0213565 5.51 0.000 .0758623 .1595781 socst | .0801873 .0194432 iv.12 0.000 .0420794 .1182952 -------------+---------------------------------------------------------------- /cut1 | 9.703706 ane.197002 7.357626 12.04979 /cut2 | 11.8001 1.304306 nine.243705 14.35649 ------------------------------------------------------------------------------
The results betoken that the overall model is statistically significant (p < .0000), as are each of the predictor variables (p < .000). At that place are 2 cutpoints for this model because there are three levels of the outcome variable.
One of the assumptions underlying ordinal logistic (and ordinal probit) regression is that the relationship between each pair of outcome groups is the same. In other words, ordinal logistic regression assumes that the coefficients that describe the human relationship betwixt, say, the everyman versus all college categories of the response variable are the aforementioned every bit those that draw the human relationship between the adjacent lowest category and all higher categories, etc. This is called the proportional odds assumption or the parallel regression assumption. Because the relationship between all pairs of groups is the same, in that location is just one gear up of coefficients (only ane model). If this was not the case, nosotros would demand different models (such as a generalized ordered logit model) to depict the relationship betwixt each pair of outcome groups. To exam this assumption, we tin can utilise either the omodel command (search omodel, run into How can I used the search control to search for programs and get boosted assistance? for more than data nigh using search) or the brant control. We will show both below.
omodel logit write3 female person read socst Iteration 0: log likelihood = -218.31357 Iteration 1: log likelihood = -158.87444 Iteration 2: log likelihood = -156.35529 Iteration three: log likelihood = -156.27644 Iteration four: log likelihood = -156.27632 Ordered logit estimates Number of obs = 200 LR chi2(3) = 124.07 Prob > chi2 = 0.0000 Log likelihood = -156.27632 Pseudo R2 = 0.2842 ------------------------------------------------------------------------------ write3 | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- female | ane.285435 .3244565 3.96 0.000 .649512 1.921358 read | .1177202 .0213564 5.51 0.000 .0758623 .159578 socst | .0801873 .0194432 4.12 0.000 .0420794 .1182952 -------------+---------------------------------------------------------------- _cut1 | 9.703706 1.197 (Ancillary parameters) _cut2 | 11.8001 1.304304 ------------------------------------------------------------------------------ Approximate likelihood-ratio test of proportionality of odds across response categories: chi2(3) = 2.03 Prob > chi2 = 0.5658 brant, item Estimated coefficients from j-ane binary regressions y>ane y>two female ane.5673604 1.0629714 read .11712422 .13401723 socst .0842684 .06429241 _cons -10.001584 -11.671854 Brant Examination of Parallel Regression Assumption Variable | chi2 p>chi2 df -------------+-------------------------- All | 2.07 0.558 three -------------+-------------------------- female person | 1.08 0.300 i read | 0.26 0.608 one socst | 0.52 0.470 i ---------------------------------------- A significant test statistic provides prove that the parallel regression assumption has been violated.
Both of these tests indicate that the proportional odds supposition has non been violated.
See also
- Stata FAQ: In ordered probit and logit, what are the cut points?
- Stata Annotated Output: Ordered logistic regression
Factorial logistic regression
A factorial logistic regression is used when you take two or more categorical contained variables but a dichotomous dependent variable. For example, using the hsb2 data file we will use female as our dependent variable, considering information technology is the merely dichotomous (0/1) variable in our information set; certainly not because it common practice to use gender as an outcome variable. We will utilise type of program (prog) and school type (schtyp) every bit our predictor variables. Because prog is a chiselled variable (it has three levels), we demand to create dummy codes for it. The employ of i.prog does this. You can use the logit command if you want to see the regression coefficients or the logistic command if y'all want to see the odds ratios.
logit female person i.prog##schtyp Iteration 0: log likelihood = -137.81834 Iteration 1: log likelihood = -136.25886 Iteration 2: log likelihood = -136.24502 Iteration 3: log likelihood = -136.24501 Logistic regression Number of obs = 200 LR chi2(v) = 3.fifteen Prob > chi2 = 0.6774 Log likelihood = -136.24501 Pseudo R2 = 0.0114 ------------------------------------------------------------------------------ female | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- prog | 2 | .3245866 .3910782 0.83 0.407 -.4419125 1.091086 3 | .2183474 .4319116 0.51 0.613 -.6281839 1.064879 | two.schtyp | 1.660724 1.141326 1.46 0.146 -.5762344 iii.897683 | prog#schtyp | 2 2 | -one.934018 i.232722 -1.57 0.117 -four.350108 .4820729 iii 2 | -1.827778 i.840256 -0.99 0.321 -5.434614 ane.779057 | _cons | -.0512933 .3203616 -0.xvi 0.873 -.6791906 .576604 ------------------------------------------------------------------------------
The results indicate that the overall model is non statistically pregnant (LR chi2 = three.15, p = 0.6774). Furthermore, none of the coefficients are statistically significant either. We can utilize the test command to get the examination of the overall effect of prog as shown beneath. This shows that the overall effect of prog is not statistically significant.
exam ii.prog 3.prog ( 1) [female]2.prog = 0 ( 2) [female person]three.prog = 0 chi2( ii) = 0.69 Prob > chi2 = 0.7086
Besides, nosotros can use the testparm command to become the test of the overall effect of the prog by schtyp interaction, as shown beneath. This shows that the overall effect of this interaction is not statistically significant.
testparm prog#schtyp ( 1) [female person]two.prog#2.schtyp = 0 ( two) [female]3.prog#2.schtyp = 0 chi2( 2) = ii.47 Prob > chi2 = 0.2902
If yous prefer, you could use the logistic command to run into the results as odds ratios, as shown below.
logistic female i.prog##schtyp Logistic regression Number of obs = 200 LR chi2(5) = 3.15 Prob > chi2 = 0.6774 Log likelihood = -136.24501 Pseudo R2 = 0.0114 ------------------------------------------------------------------------------ female | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- prog | ii | one.383459 .5410405 0.83 0.407 .6428059 2.977505 three | 1.244019 .5373063 0.51 0.613 .5335599 2.900487 | two.schtyp | 5.263121 6.006939 i.46 0.146 .5620107 49.28811 | prog#schtyp | two 2 | .1445662 .1782099 -1.57 0.117 .0129054 ane.619428 three 2 | .1607704 .2958586 -0.99 0.321 .0043629 5.924268 ------------------------------------------------------------------------------
Correlation
A correlation is useful when yous want to see the linear relationship between two (or more than) usually distributed interval variables. For case, using the hsb2 information file we can run a correlation between 2 continuous variables, read and write.
corr read write
(obs=200) | read write -------------+------------------ read | i.0000 write | 0.5968 1.0000
In the second case, nosotros will run a correlation betwixt a dichotomous variable, female, and a continuous variable, write. Although it is assumed that the variables are interval and unremarkably distributed, nosotros can include dummy variables when performing correlations.
corr female write
(obs=200) | female write -------------+------------------ female | 1.0000 write | 0.2565 1.0000
In the beginning instance above, nosotros meet that the correlation between read and write is 0.5968. Past squaring the correlation so multiplying by 100, you can determine what percent of the variability is shared. Let'due south round 0.5968 to be 0.6, which when squared would be .36, multiplied by 100 would be 36%. Hence read shares about 36% of its variability with write. In the output for the second case, nosotros can see the correlation between write and female is 0.2565. Squaring this number yields .06579225, meaning that female shares approximately 6.5% of its variability with write.
See likewise
- Annotated Stata Output: Correlation
- Stata Instruction Tools
- Stata Learning Module: A Statistical Sampler in Stata
- Stata Programs for Data Analysis
- Stata Course Notes: Exploring Data
- Stata Class Notes: Analyzing Data
Elementary linear regression
Simple linear regression allows us to look at the linear relationship between one normally distributed interval predictor and one normally distributed interval outcome variable. For case, using the hsb2 information file, say we wish to expect at the relationship between writing scores (write) and reading scores (read); in other words, predicting write from read.
regress write read ------------------------------------------------------------------------------ write | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- read | .5517051 .0527178 ten.47 0.000 .4477446 .6556656 _cons | 23.95944 ii.805744 viii.54 0.000 eighteen.42647 29.49242 ------------------------------------------------------------------------------
We see that the human relationship betwixt write and read is positive (.5517051) and based on the t-value (10.47) and p-value (0.000), we would conclude this relationship is statistically significant. Hence, we would say there is a statistically significant positive linear relationship between reading and writing.
Run across also
- Regression With Stata: Chapter 1 – Simple and Multiple Regression
- Stata Annotated Output: Regression
- Stata Frequently Asked Questions
- Stata Textbook Examples: Regression with Graphics, Chapter two
- Stata Textbook Examples: Applied Regression Analysis, Chapter 5
Non-parametric correlation
A Spearman correlation is used when one or both of the variables are not assumed to be normally distributed and interval (merely are assumed to be ordinal). The values of the variables are converted in ranks and so correlated. In our instance, we will expect for a relationship betwixt read and write. We will non presume that both of these variables are normal and interval .
spearman read write
Number of obs = 200 Spearman'due south rho = 0.6167 Exam of Ho: read and write are contained Prob > |t| = 0.0000
The results suggest that the relationship between read and write (rho = 0.6167, p = 0.000) is statistically meaning.
Simple logistic regression
Logistic regression assumes that the upshot variable is binary (i.e., coded as 0 and 1). We have only 1 variable in the hsb2 information file that is coded 0 and ane, and that is female. We empathise that female person is a light-headed outcome variable (it would brand more sense to utilize information technology as a predictor variable), but we can use female equally the event variable to illustrate how the code for this control is structured and how to interpret the output. The first variable listed afterwards the logistic (or logit) command is the event (or dependent) variable, and all of the remainder of the variables are predictor (or contained) variables. You can use the logit control if you want to encounter the regression coefficients or the logistic command if you want to see the odds ratios. In our example, female person volition be the consequence variable, and read will be the predictor variable. Equally with OLS regression, the predictor variables must be either dichotomous or continuous; they cannot be categorical.
logistic female read Logit estimates Number of obs = 200 LR chi2(1) = 0.56 Prob > chi2 = 0.4527 Log likelihood = -137.53641 Pseudo R2 = 0.0020 ------------------------------------------------------------------------------ female | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- read | .9896176 .0137732 -0.75 0.453 .9629875 1.016984 ------------------------------------------------------------------------------ logit female read
Iteration 0: log likelihood = -137.81834 Iteration 1: log likelihood = -137.53642 Iteration 2: log likelihood = -137.53641 Logit estimates Number of obs = 200 LR chi2(i) = 0.56 Prob > chi2 = 0.4527 Log likelihood = -137.53641 Pseudo R2 = 0.0020 ------------------------------------------------------------------------------ female | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- read | -.0104367 .0139177 -0.75 0.453 -.0377148 .0168415 _cons | .7260875 .7419612 0.98 0.328 -.7281297 2.180305 ------------------------------------------------------------------------------
The results indicate that reading score (read) is non a statistically significant predictor of gender (i.e., existence female), z = -0.75, p = 0.453. Also, the exam of the overall model is not statistically significant, LR chi-squared 0.56, p = 0.4527.
See also
- Stata Textbook Examples: Applied Logistic Regression (2nd Ed) Chapter 1
- Stata Spider web Books: Logistic Regression in Stata
- Stata Information Analysis Instance: Logistic Regression
- Annotated Stata Output: Logistic Regression Analysis
- Stata FAQ: How do I interpret odds ratios in logistic regression?
- Stata Library
- Didactics Tools: Graph Logistic Regression Curve
Multiple regression
Multiple regression is very similar to uncomplicated regression, except that in multiple regression y'all have more than i predictor variable in the equation. For example, using the hsb2 data file we will predict writing score from gender (female), reading, math, scientific discipline and social studies (socst) scores.
regress write female person read math scientific discipline socst
Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 5, 194) = 58.60 Model | 10756.9244 5 2151.38488 Prob > F = 0.0000 Residual | 7121.9506 194 36.7110855 R-squared = 0.6017 -------------+------------------------------ Adj R-squared = 0.5914 Total | 17878.875 199 89.843593 Root MSE = 6.059 ------------------------------------------------------------------------------ write | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- female person | five.492502 .8754227 6.27 0.000 three.765935 7.21907 read | .1254123 .0649598 i.93 0.055 -.0027059 .2535304 math | .2380748 .0671266 three.55 0.000 .1056832 .3704665 scientific discipline | .2419382 .0606997 three.99 0.000 .1222221 .3616542 socst | .2292644 .0528361 four.34 0.000 .1250575 .3334713 _cons | 6.138759 two.808423 2.19 0.030 .599798 eleven.67772 ------------------------------------------------------------------------------
The results indicate that the overall model is statistically significant (F = 58.60, p = 0.0000). Furthermore, all of the predictor variables are statistically significant except for read.
See also
- Regression with Stata: Lesson 1 – Uncomplicated and Multiple Regression
- Annotated Output: Multiple Linear Regression
- Stata Annotated Output: Regression
- Stata Teaching Tools
- Stata Textbook Examples: Applied Linear Statistical Models
- Stata Textbook Examples: Regression Analysis by Instance, Chapter 3
Analysis of covariance
Assay of covariance is like ANOVA, except in add-on to the categorical predictors you also have continuous predictors every bit well. For instance, the one fashion ANOVA instance used write as the dependent variable and prog equally the contained variable. Allow's add together read as a continuous variable to this model, as shown below.
anova write prog c.read Number of obs = 200 R-squared = 0.3925 Root MSE = vii.44408 Adj R-squared = 0.3832 Source | Partial SS df MS F Prob > F -----------+---------------------------------------------------- Model | 7017.68123 iii 2339.22708 42.21 0.0000 | prog | 650.259965 2 325.129983 5.87 0.0034 read | 3841.98338 1 3841.98338 69.33 0.0000 | Residual | 10861.1938 196 55.4142539 ----------+---------------------------------------------------- Full | 17878.875 199 89.843593
The results indicate that even later adjusting for reading score (read), writing scores notwithstanding significantly differ by program type (prog) F = five.87, p = 0.0034.
See also
- Stata Textbook Examples: Design and Analysis, Chapter xiv
- Stata Code Fragment: ANOVA
Multiple logistic regression
Multiple logistic regression is like simple logistic regression, except that in that location are two or more predictors. The predictors can be interval variables or dummy variables, merely cannot exist categorical variables. If you lot have chiselled predictors, they should be coded into ane or more dummy variables. Nosotros take only i variable in our data gear up that is coded 0 and 1, and that is female person. We empathise that female is a silly outcome variable (it would make more than sense to utilise information technology as a predictor variable), but we can use female as the upshot variable to illustrate how the code for this command is structured and how to interpret the output. The first variable listed subsequently the logistic (or logit) command is the outcome (or dependent) variable, and all of the rest of the variables are predictor (or contained) variables. You can apply the logit command if you want to see the regression coefficients or the logistic command if you want to come across the odds ratios. In our instance, female volition be the event variable, and read and write will exist the predictor variables.
logistic female read write Logit estimates Number of obs = 200 LR chi2(ii) = 27.82 Prob > chi2 = 0.0000 Log likelihood = -123.90902 Pseudo R2 = 0.1009 ------------------------------------------------------------------------------ female | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- read | .9314488 .0182578 -3.62 0.000 .8963428 .9679298 write | i.112231 .0246282 4.fourscore 0.000 i.064993 1.161564 ------------------------------------------------------------------------------
These results evidence that both read and write are significant predictors of female.
See also
- Stata Annotated Output: Logistic Regression
- Stata Library
- Stata Spider web Books: Logistic Regression with Stata
- Stata Textbook Examples: Applied Logistic Regression, Affiliate 2
- Stata Textbook Examples: Applied Regression Analysis, Affiliate eight
- Stata Textbook Examples: Introduction to Categorical Analysis, Chapter v
- Stata Textbook Examples: Regression Analysis by Case, Chapter 12
Discriminant analysis
Discriminant analysis is used when y'all have one or more commonly distributed interval independent variables and a categorical dependent variable. It is a multivariate technique that considers the latent dimensions in the independent variables for predicting group membership in the categorical dependent variable. For instance, using the hsb2 information file, say we wish to utilize read, write and math scores to predict the type of plan a student belongs to (prog). For this analysis, you demand to first download the daoneway programme that performs this exam. You tin can download daoneway from inside Stata by typing search daoneway (encounter How can I used the search command to search for programs and get additional help? for more than data almost using search).
You can then perform the discriminant part analysis like this.
daoneway read write math, by(prog)
One-way Disciminant Function Analysis Observations = 200 Variables = iii Groups = three Percentage of Cum Approved After Wilks' Fcn Eigenvalue Variance Percentage Corr Fcn Lambda Chi-square df P-value | 0 0.73398 60.619 6 0.0000 1 0.3563 98.74 98.74 0.5125 | 1 0.99548 0.888 two 0.6414 2 0.0045 one.26 100.00 0.0672 | Unstandardized canonical discriminant function coefficients func1 func2 read 0.0292 -0.0439 write 0.0383 0.1370 math 0.0703 -0.0793 _cons -7.2509 -0.7635 Standardized approved discriminant function coefficients func1 func2 read 0.2729 -0.4098 write 0.3311 1.1834 math 0.5816 -0.6557 Canonical discriminant structure matrix func1 func2 read 0.7785 -0.1841 write 0.7753 0.6303 math 0.9129 -0.2725 Group means on canonical discriminant functions func1 func2 prog-i -0.3120 0.1190 prog-two 0.5359 -0.0197 prog-3 -0.8445 -0.0658
Conspicuously, the Stata output for this procedure is lengthy, and it is beyond the scope of this folio to explain all of information technology. However, the main point is that two canonical variables are identified by the assay, the first of which seems to exist more related to program type than the 2d.
See also
- Stata Information Analysis Examples: Discriminant Function Assay
One-way MANOVA
MANOVA (multivariate analysis of variance) is like ANOVA, except that there are two or more dependent variables. In a one-mode MANOVA, in that location is one chiselled independent variable and two or more dependent variables. For case, using the hsb2 data file, say we wish to examine the differences in read, write and math cleaved down past program type (prog). For this analysis, you tin utilize the manova command and then perform the analysis like this.
manova read write math = prog, category(prog)
Number of obs = 200 W = Wilks' lambda 50 = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+-------------------------------------------------- prog | W 0.7340 ii 6.0 390.0 ten.87 0.0000 e | P 0.2672 vi.0 392.0 10.08 0.0000 a | L 0.3608 6.0 388.0 11.67 0.0000 a | R 0.3563 iii.0 196.0 23.28 0.0000 u |-------------------------------------------------- Residual | 197 -----------+-------------------------------------------------- Total | 199 -------------------------------------------------------------- e = exact, a = judge, u = upper bound on F
This command produces three unlike examination statistics that are used to evaluate the statistical significance of the relationship between the independent variable and the effect variables. According to all three criteria, the students in the unlike programs differ in their joint distribution of read, write and math. See also
- Stata Data Assay Examples: One-way MANOVA
- Stata Annotated Output: One-style MANOVA
- Stata FAQ: How can I exercise multivariate repeated measures in Stata?
Multivariate multiple regression
Multivariate multiple regression is used when you have two or more dependent variables that are to exist predicted from two or more than predictor variables. In our example, we will predict write and read from female, math, science and social studies (socst) scores.
mvreg write read = female math science socst
Equation Obs Parms RMSE "R-sq" F P ---------------------------------------------------------------------- write 200 5 6.101191 0.5940 71.32457 0.0000 read 200 v 6.679383 0.5841 68.4741 0.0000 ------------------------------------------------------------------------------ | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- write | female | v.428215 .8808853 vi.16 0.000 3.69093 7.165501 math | .2801611 .0639308 4.38 0.000 .1540766 .4062456 science | .2786543 .0580452 four.80 0.000 .1641773 .3931313 socst | .2681117 .049195 5.45 0.000 .1710892 .3651343 _cons | vi.568924 ii.819079 2.33 0.021 i.009124 12.12872 -------------+---------------------------------------------------------------- read | female | -.512606 .9643644 -0.53 0.596 -2.414529 1.389317 math | .3355829 .0699893 4.79 0.000 .1975497 .4736161 scientific discipline | .2927632 .063546 4.61 0.000 .1674376 .4180889 socst | .3097572 .0538571 5.75 0.000 .2035401 .4159744 _cons | iii.430005 3.086236 1.xi 0.268 -2.656682 9.516691 ------------------------------------------------------------------------------
Many researchers familiar with traditional multivariate assay may non recognize the tests to a higher place. They practice not come across Wilks' Lambda, Pillai'south Trace or the Hotelling-Lawley Trace statistics, the statistics with which they are familiar. It is possible to obtain these statistics using the mvtest command written by David Eastward. Moore of the Academy of Cincinnati. UCLA updated this command to work with Stata 6 and above. You lot tin download mvtest from inside Stata past typing search mvtest (come across How can I used the search command to search for programs and get additional help? for more than data nigh using search).
At present that nosotros take downloaded it, nosotros tin use the command shown below.
mvtest female
MULTIVARIATE TESTS OF SIGNIFICANCE Multivariate Examination Criteria and Exact F Statistics for the Hypothesis of no Overall "female" Effect(s) S=one M=0 Due north=96 Examination Value F Num DF Den DF Pr > F Wilks' Lambda 0.83011470 19.8513 two 194.0000 0.0000 Pillai'due south Trace 0.16988530 19.8513 ii 194.0000 0.0000 Hotelling-Lawley Trace 0.20465280 19.8513 2 194.0000 0.0000
These results show that female has a significant human relationship with the articulation distribution of write and read. The mvtest command could so be repeated for each of the other predictor variables.
Run across besides
- Regression with Stata: Chapter 4, Across OLS
- Stata Data Analysis Examples: Multivariate Multiple Regression
- Stata Textbook Examples, Econometric Analysis, Affiliate 16
Canonical correlation
Canonical correlation is a multivariate technique used to examine the relationship betwixt two groups of variables. For each set of variables, information technology creates latent variables and looks at the relationships amongst the latent variables. Information technology assumes that all variables in the model are interval and normally distributed. Stata requires that each of the two groups of variables be enclosed in parentheses. At that place need not be an equal number of variables in the two groups.
catechism (read write) (math science) Linear combinations for canonical correlation 1 Number of obs = 200 ------------------------------------------------------------------------------ | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- u | read | .0632613 .007111 8.90 0.000 .0492386 .077284 write | .0492492 .007692 6.40 0.000 .0340809 .0644174 -------------+---------------------------------------------------------------- five | math | .0669827 .0080473 8.32 0.000 .0511138 .0828515 science | .0482406 .0076145 6.34 0.000 .0332252 .0632561 ------------------------------------------------------------------------------ (Std. Errors estimated conditionally) Canonical correlations: 0.7728 0.0235
The output above shows the linear combinations corresponding to the showtime approved correlation. At the lesser of the output are the 2 canonical correlations. These results signal that the offset canonical correlation is .7728. You lot will note that Stata is cursory and may not provide you with all of the information that y'all may desire. Several programs have been developed to provide more than information regarding the analysis. You can download this family of programs by typing search cancor (see How can I used the search command to search for programs and get additional assist? for more information about using search).
Because the output from the cancor command is lengthy, nosotros will employ the cantest command to obtain the eigenvalues, F-tests and associated p-values that nosotros want. Note that you practise not have to specify a model with either the cancor or the cantest commands if they are issued after the canon command.
cantest
Canon Tin can Corr Likelihood Approx Corr Squared Ratio F df1 df2 Pr > F 7728 .59728 0.4025 56.4706 iv 392.000 0.0000 0235 .00055 0.9994 0.1087 1 197.000 0.7420 Eigenvalue Proportion Cumulative 1.4831 0.9996 0.9996 0.0006 0.0004 one.0000
The F-examination in this output tests the hypothesis that the first canonical correlation is equal to zero. Conspicuously, F = 56.4706 is statistically meaning. Nonetheless, the 2nd canonical correlation of .0235 is non statistically significantly unlike from nothing (F = 0.1087, p = 0.7420).
See also
- Stata Data Analysis Examples: Approved Correlation Analysis
- Stata Annotated Output: Canonical Correlation Analysis
- Stata Textbook Examples: Computer-Aided Multivariate Analysis, Affiliate 10
Factor assay
Cistron analysis is a form of exploratory multivariate assay that is used to either reduce the number of variables in a model or to find relationships amidst variables. All variables involved in the gene analysis demand to be continuous and are assumed to be ordinarily distributed. The goal of the analysis is to endeavor to identify factors which underlie the variables. There may be fewer factors than variables, only there may not be more than factors than variables. For our case, allow's suppose that nosotros retrieve that there are some common factors underlying the various exam scores. We volition start use the main components method of extraction (by using the pc pick) and then the principal components gene method of extraction (by using the pcf selection). This parallels the output produced by SAS and SPSS.
gene read write math science socst, pc (obs=200) (principal components; 5 components retained) Component Eigenvalue Difference Proportion Cumulative ------------------------------------------------------------------ 1 3.38082 2.82344 0.6762 0.6762 2 0.55738 0.15059 0.1115 0.7876 iii 0.40679 0.05062 0.0814 0.8690 four 0.35617 0.05733 0.0712 0.9402 5 0.29884 . 0.0598 1.0000 Eigenvectors Variable | 1 2 3 4 5 -------------+------------------------------------------------------ read | 0.46642 -0.02728 -0.53127 -0.02058 -0.70642 write | 0.44839 0.20755 0.80642 0.05575 -0.32007 math | 0.45878 -0.26090 -0.00060 -0.78004 0.33615 science | 0.43558 -0.61089 -0.00695 0.58948 0.29924 socst | 0.42567 0.71758 -0.25958 0.20132 0.44269
At present let'due south rerun the factor analysis with a main component factors extraction method and retain factors with eigenvalues of .five or greater. So nosotros will use a varimax rotation on the solution.
cistron read write math scientific discipline socst, pcf mineigen(.5) (obs=200) (principal component factors; 2 factors retained) Factor Eigenvalue Difference Proportion Cumulative ------------------------------------------------------------------ 1 three.38082 two.82344 0.6762 0.6762 2 0.55738 0.15059 0.1115 0.7876 3 0.40679 0.05062 0.0814 0.8690 4 0.35617 0.05733 0.0712 0.9402 5 0.29884 . 0.0598 one.0000 Factor Loadings Variable | one 2 Uniqueness -------------+-------------------------------- read | 0.85760 -0.02037 0.26410 write | 0.82445 0.15495 0.29627 math | 0.84355 -0.19478 0.25048 scientific discipline | 0.80091 -0.45608 0.15054 socst | 0.78268 0.53573 0.10041
rotate, varimax (varimax rotation) Rotated Gene Loadings Variable | 1 2 Uniqueness -------------+-------------------------------- read | 0.64808 0.56204 0.26410 write | 0.50558 0.66942 0.29627 math | 0.75506 0.42357 0.25048 scientific discipline | 0.89934 0.20159 0.15054 socst | 0.21844 0.92297 0.10041
Annotation that by default, Stata will retain all factors with positive eigenvalues; hence the apply of the mineigen option or the factors(#) option. The factors(#) selection does not specify the number of solutions to retain, but rather the largest number of solutions to retain. From the table of cistron loadings, nosotros tin can see that all five of the test scores load onto the first factor, while all five tend to load non and so heavily on the second factor. Uniqueness (which is the opposite of commonality) is the proportion of variance of the variable (i.e., read) that is not accounted for by all of the factors taken together, and a very high uniqueness can indicate that a variable may not belong with whatsoever of the factors. Factor loadings are often rotated in an attempt to make them more than interpretable. Stata performs both varimax and promax rotations.
rotate, varimax
(varimax rotation) Rotated Gene Loadings Variable | 1 2 Uniqueness -------------+-------------------------------- read | 0.62238 0.51992 0.34233 write | 0.53933 0.54228 0.41505 math | 0.65110 0.45408 0.36988 scientific discipline | 0.64835 0.37324 0.44033 socst | 0.44265 0.58091 0.46660
The purpose of rotating the factors is to get the variables to load either very high or very depression on each gene. In this case, because all of the variables loaded onto factor one and not on factor 2, the rotation did not aid in the interpretation. Instead, it made the results even more than difficult to interpret.
To obtain a scree plot of the eigenvalues, you lot can use the greigen command. Nosotros have included a reference line on the y-axis at one to aid in determining how many factors should be retained.
greigen, yline(1)
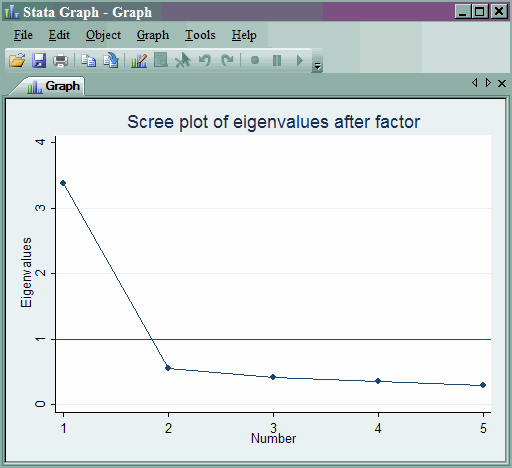
Run across as well
- Stata Annotated Output: Cistron Analysis
- Stata Textbook Examples, Regression with Graphics, Affiliate 8
Source: https://stats.oarc.ucla.edu/stata/whatstat/what-statistical-analysis-should-i-usestatistical-analyses-using-stata/
0 Response to "Not All Independent Variables Can Be Retained in Binary Logits Brant Test Cannot Be Computed"
Post a Comment